I'll Tell You How This Can Be True.

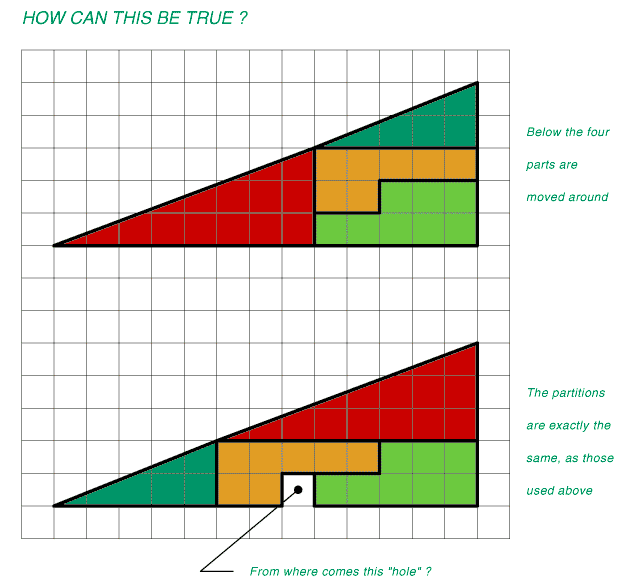
I've seen this "paradox" on the web many times now in more than one language and I've yet to see anyone posting the solution. The fact that it keeps getting reposted leads me to believe that people actually think this is a genuine paradox when in fact it doesn't take more than grade 8 math to figure out what is "wrong" (although, admittedly, it isn't obvious at first glance).

** start grade 8 math **

The area of a right-angle triangle is one half of the area of the rectangle with the same length sides.

So:

(13 * 5 ) / 2 = 32.5

Now look at the individual shapes:

The green triangle: (5 * 2 ) / 2 = 5

The red triangle: (8 * 3) / 2 = 12

The yellow "L" shape has 7 squares.

The green "L" shape has 8 squares.

5 + 12 + 7 + 8 = 32

The area of the top shape is 32 squares, not the 32.5 is should be if it was a right angle triangle.

Likewise the area of the bottom shape, with the "paradoxical" extra square is 33 squares, not the 32.5 is should be if it were a right angle triangle.

Neither shape is a right angle triangle.

The small green triangle and the large red triangle in the two shapes do not have the same proportions.

5:2 ≠ 8:3

Using a common denominator to show this:

(5 * 3) : (2 * 3) ≠ (8 * 2) : (3 * 2)

15:6 ≠ 16:6

Obviously the angles in a 15:6 triangle are not going to be the same as a 16:6 triangle.

** end grade 8 math **

Now if you want to get into the heady world of *gasp* high-school algebra to get into more detail:

The 13 x 5 triangle, using Pythagoras (a² + b² = c²), has a hypotenuse of 13.928 units and (simple trigonometry) interior angles of 21.04°, 90°, and 68.96°.

The small green 5 x 2 triangle has a hypotenuse of 5.385 units and interior angles of 21.8°, 90°, and 68.2°.

The small red 8 x 3 triangle has a hypotenuse of 8.544 units and interior angles of 20.56°, 90°, and 69.44°.

We have a very obtuse triangle with sides that are 5.385, 8.544 and 13.928 units long and interior angles of 178.76°, 0.48°, and 0.76° "left over".

You'll find this "leftover" happens to have an area of one half square.

The upper shape "dents in" below the true hypotenuse of the 13 x 5 triangle by the dimensions of this obtuse triangle, making it "short" half a square in area.

Conversely the lower shape "bulges" above the true hypotenuse of the 13 x 5 triangle by the same amount, making it "over" half a square in area.